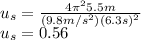Question

A cat dozes on a stationary merry-go-round, at a radius of 5.5 m from the center of the ride. Then the operator turns on the ride and brings it up to its proper turning rate of one complete rotation every 6.3 s. What is the least coefficient of static friction between the cat and the merry-go-round that will allow the cat to stay in place, without sliding

Answer 1

`u_(s)=0.56`

Step-by-step explanation:

For the cat to stay in place on the merry go round without sliding the magnitude of maximum static friction must be equal to magnitude of centripetal force

`F_(s.max)=(mv^2)/(r) \\`

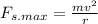
Where the r is the radius of merry-go-round and v is the tangential speed

but

`F_(s.max)=u_(s)F_(N)=u_(s)mg`

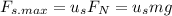
So we have

`u_(s)mg=(mv^2)/(r)\\ u_(s)=(v^2)/(gr)\\ Where\\v=(2\pi R)/(T) \\So\\u_(s)=(((2\pi R)/(T) )^2)/(gr) \\u_(s)=(4\pi^2 r)/(gT^2)`

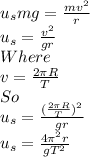
Substitute the given values

So

`u_(s)=(4\pi^2 5.5m)/((9.8m/s^2)(6.3s)^2) \\u_(s)=0.56`