a)
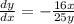
b)
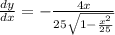
c) The two expressions match
Answer:
a)
The equation in this problem is
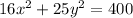
Here, we want to find
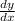 by implicit differentiation.
by implicit differentiation.
To do that, we apply the operator
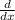 on each term of the equation. We have:
on each term of the equation. We have:
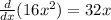
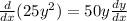 (by applying composite function rule)
(by applying composite function rule)
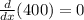
Therefore, the equation becomes:
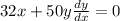
And re-arranging for dy/dx, we get:
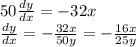
b)
Now we want to solve the equation explicitly for y and then differentiate to find dy/dx. The equation is:
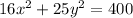
First, we isolate y, and we find:
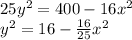
And taking the square root,
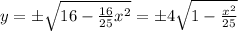
Here we are told to consider only the first and second quadrants, so those where y > 0; so we only take the positive root:
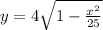
Now we differentiate this function to find dy/dx; using the chain rule, we get:
![(dy)/(dx)=4[(1)/(2)(1-(x^2)/(25))^{-(1)/(2)}\cdot(-(2x)/(25))]=-\frac{4x}{25\sqrt{1-(x^2)/(25)}}](https://img.qammunity.org/2021/formulas/mathematics/college/quo9fmms980jmgg5n0smmvpbazgkvaf2fd.png) (2)
(2)
c)
Now we want to check if the two solutions are consistent.
To do that, we substitute the expression that we found for y in part b:
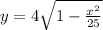
Into the solution found in part a:
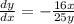
Doing so, we find:
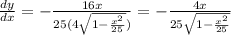 (1)
(1)
We observe that expression (1) matches with expression (2) found in part b: therefore, we can conclude that the two solutions are coeherent with each other.