Question

An equilateral triangle is inscribed in a circle of radius 6r. Express the area A within the circle but outside the triangle as a function of the length 5x of the side of the triangle.

Answer 1

`A(x)=(100\pi x^2-75√(3)x^2)/(12)`

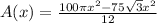
Explanation:

We have been given that an equilateral triangle is inscribed in a circle of radius 6r. We are asked to express the area A within the circle but outside the triangle as a function of the length 5x of the side of the triangle.

We know that the relation between radius (R) of circumscribing circle to the side (a) of inscribed equilateral triangle is
`(a)/(√(3))=R`.

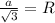Upon substituting our given values, we will get:

`(5x)/(√(3))=6r`

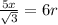
Let us solve for r.

`r=(5x)/(6√(3))`

`\text{Area of circle}=\pi(6r)^2=\pi(6\cdot (5x)/(6√(3)))^2=\pi((5x)/(√(3)))^2=(25\pi x^2)/(3)`

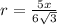
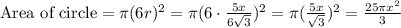
We know that area of an equilateral triangle is equal to
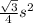`(√(3))/(4)s^2`, where s represents side length of triangle.

`\text{Area of equilateral triangle}=(√(3))/(4)s^2=(√(3))/(4)(5x)^2=(25√(3))/(4)x^2`

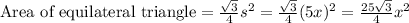
The area within circle and outside the triangle would be difference of area of circle and triangle as:

`A(x)=(25\pi x^2)/(3)-(25√(3)x^2)/(4)`

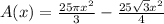
We can make a common denominator as:

`A(x)=(4\cdot 25\pi x^2)/(12)-(3\cdot 25√(3)x^2)/(12)`

`A(x)=(100\pi x^2-75√(3)x^2)/(12)`

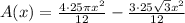
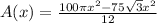
Therefore, our required expression would be
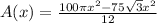`A(x)=(100\pi x^2-75√(3)x^2)/(12)`.