Question

Alvin paddled for 2 hours with a 8​-km/h current to reach a campsite. The return trip against the same current took 10 hours. Find the speed of the boat in still water.

Answer 1

The speed of the boat in still water is 12km/h.

Step-by-step explanation:

This is a relative motion problem. The boat is moving relative to the water, which is moving relative to the ground. We can express this with the formula:

`v_(b/0)=v_(b/w)+v_(w/0)`

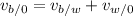
Where
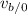`v_(b/0)` is the speed of the boat relative to the ground,
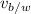`v_(b/w)` is the speed of the boat relative to the water, and
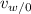`v_(w/0)` is the speed of the water relative to the ground.

We have that
`v_(w/0)=8km/h` and that, in the first trip
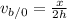`v_(b/0)=(x)/(2h)` and in the second trip
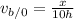`v_(b/0)=(x)/(10h)`, where x is the distance traveled. Also, in the first trip
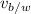`v_(b/w)` and
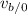`v_(b/0)` are positive and in the second one are negative (because the boat goes in opposite directions). So, using some mathematics, we can say that:

`(x)/(2h) =v_(b/w)+8km/h; -(x)/(10h) =-v_(b/w)+8km/h\\\\x=2h(v_(b/w)+8km/h);x=-10h(-v_(b/w)+8km/h)\\\\\implies 2h(v_(b/w)+8km/h)=-10h(-v_(b/w)+8km/h)\\\\-4v_(b/w)=-48km/h\\\\v_(b/w)=12km/h`

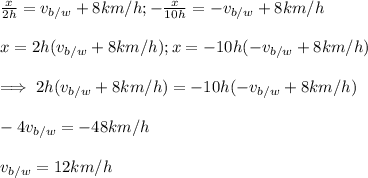
This means that the speed of the boat relative to the water is 12km/h. This is independent to the speed of water, so the speed of the boat in still water is 12km/h.