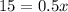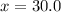Question

The range of the random variable X is {1, 10, 15, 20, 25, x} where x is unknown. The value x has probability 0.50 and each of the remaining values has probability 0.10. The expected value of X is 22.1. Determine x. Answer to 1 decimal places.

Answer 1

`22.1 = 1*0.1 +10*0.1 +15*0.1 + 20*0.1 +25*0.1 + x*0.5`

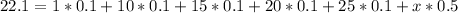
And we can solve for the value of x and we got:

`22.1 -[1*0.1 +10*0.1 +15*0.1 + 20*0.1 +25*0.1 ] = 0.5 x`

`15 = 0.5 x`

`x =30.0`

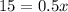
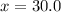
Explanation:

For this case we have the following distribution:

X 1 10 15 20 25 x

P(X) 0.1 0.1 0.1 0.1 0.1 0.5

The expected value of a random variable X is the n-th moment about zero of a probability density function f(x) if X is continuous, or the weighted average for a discrete probability distribution, if X is discrete.

The variance of a random variable X represent the spread of the possible values of the variable. The variance of X is written as Var(X).

The expected value is given by:

`E(X) = \sum_(i=1)^n X_i P(X_i)`

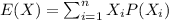
And replacing we have this:

`22.1 = 1*0.1 +10*0.1 +15*0.1 + 20*0.1 +25*0.1 + x*0.5`

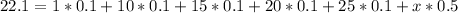
And we can solve for the value of x and we got:

`22.1 -[1*0.1 +10*0.1 +15*0.1 + 20*0.1 +25*0.1 ] = 0.5 x`

`15 = 0.5 x`

`x =30.0`