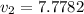Answer:

Explanation:
Consider car 1 with mass
 and original speed
and original speed
 and car 2 with mass
and car 2 with mass
 and original speed
and original speed
 . We can consider both cars as punctual masses. In this case, recall that the kinetic energy of a particle of mass
. We can consider both cars as punctual masses. In this case, recall that the kinetic energy of a particle of mass
 and speed
and speed
 is given by the expression
is given by the expression
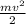 . Then, since car 1 has twice the mass of a second car, but only half as much kinetic energy based on the description, we have the following equations.
. Then, since car 1 has twice the mass of a second car, but only half as much kinetic energy based on the description, we have the following equations.
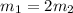 ,
,
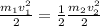 .
.
Replacing the equation
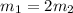 in the second one, leads to
in the second one, leads to
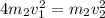 , which implies
, which implies
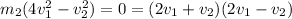 Since
Since
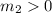 and assuming that both speeds are positive, then
and assuming that both speeds are positive, then
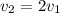 .
.
Given that, if both cars increase their speed by 5.5 m/s then they have the same kinetic energy, we have that
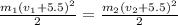 . Using the previous result, and expressing everything in terms of
. Using the previous result, and expressing everything in terms of
 and
and
 we have that
we have that
 (where
(where
 cancells out).
cancells out).
Then, we have the following equation
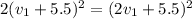 , which by algebraic calculations leads to
, which by algebraic calculations leads to
![v_1 = \pm \frac{5.5}{\sqrt[]{2}} = \pm 3.8891](https://img.qammunity.org/2021/formulas/mathematics/college/z2imbpxtsjignasygmu76c9kagg5n56974.png) . Since we assumed
. Since we assumed
 , we have that
, we have that
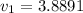 .Then,
.Then,