Question

A hedge fund returns on average 26% per year with a standard deviation of 12%. Using the empirical rule, approximate the probability the fund returns over 50% next year

Answer 1

0.025 is the probability that the fund returns over 50% next year.

Step-by-step explanation:

We are given the following information in the question:

Mean, μ = 26%

Standard Deviation, σ = 12%

Empirical Formula:

• Almost all the data lies within three standard deviation from the mean for a normal data.
• About 68% of data lies within one standard deviation of the mean.
• Around 95% of data lies within two standard deviation of the mean.
• About 99.7% of data lies within three standard deviations of mean.
• The mean divide the data into two equal parts.

We have to find the approximate probability of the fund returns over 50% next year.

`P(x > 50)\\=P(x > 26\% + 2(12\%))\\=P(x > \mu + 2\sigma)\\\\=0.5 - (P(\mu + 2\sigma <x < \mu + 2\sigma))/(2)\\\\=0.5 - (0.95)/(2)\\\\=0.025`

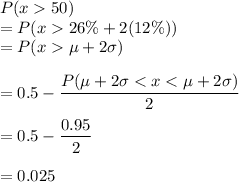
0.025 is the probability that the fund returns over 50% next year.