Question

Scientists are experimenting with a kind of gun that may eventually be used to fire payloads directly into orbit. In one test, this gun accelerates a 3.8-kg projectile from rest to a speed of 9.3 × 103 m/s. The net force accelerating the projectile is 9.3 × 105 N. How much time is required for the projectile to come up to speed?

Answer 1

`t=0.038s`

Step-by-step explanation:

Project mass m=3.8 kg

Initial speed vi= 0m/s

Final speed vf= 9.3×10³ m/s

Force F=9.3×10⁵N

To find

Time t

Solution

From Newtons second law we know that

∑F=ma

Where m is mass

a is acceleration

We can write this equation as

∑F=m(Δv/Δt)

`=m(v_(f)-v_(i))/(t)`

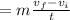
Rearrange this equation to find time t

So

`t=m(v_(f)-v_(i))/(F)`

Substitute the given values

`t=3.8kg(9.3*10^3m/s-0)/(9.3*10^5N) \\t=0.038s`