Question

Problem PageQuestion Working together, two pumps can drain a certain pool in hours. If it takes the older pump hours to drain the pool by itself, how long will it take the newer pump to drain the pool on its own?

Answer 1

10.5 hours.

Explanation:

Please consider the complete question.

Working together, two pumps can drain a certain pool in 6 hours. If it takes the older pump 14 hours to drain the pool by itself, how long will it take the newer pump to drain the pool on its own?

Let t represent time taken by newer pump in hours to drain the pool on its own.

So part of pool drained by newer pump in one hour would be
`(1)/(t)`.

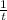We have been given that it takes the older pump 14 hours to drain the pool by itself, so part of pool drained by older pump in one hour would be
`(1)/(14)`.

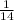Part of pool drained by both pumps working together in one hour would be
`(1)/(6)`.

Now, we will equate the sum of part of pool emptied by both pumps with
`(1)/(6)` and solve for t as:

`(1)/(14)+(1)/(t)=(1)/(6)`

`(1)/(14)* 42t+(1)/(t)* 42t=(1)/(6)* 42t`

`3t+42=7t`

`7t=3t+42`

`7t-3t=3t-3t+42`

`4t=42`

`(4t)/(4)=(42)/(4)`

`t=10.5`

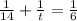
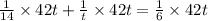
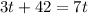
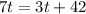
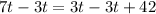
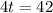
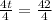
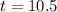
Therefore, it will take 10.5 hours for the newer pump to drain the pool on its own.