Question

Two large parallel conducting plates are 8.0 cm apart and carry equal but opposite charges on their facing surfaces. The magnitude of the surface charge density on either of the facing surfaces is 2.0 nC/m2 . Determine the magnitude of the electric potential difference between the plates.

Answer 1

To solve this problem we will use the definitions given for the electric field and the voltage. The first can be defined as a relation between the charge density and the permittivity constant in free space, while the second is related to the distance by the electric field. Finally we will replace the values and find the value of the electric potential.

Our values are,

`d = 8.0cm = 8*10^(-2) m`

`\sigma = 2.0nC/m^2 =2.0*10^(-9)C/m^2`

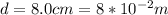
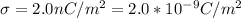
The electric field between plates is given under the equation,

`E = (\sigma)/(\epsilon_0)`

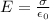
Here,

`\sigma` = Charge density

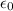`\epsilon_0`= Permittivity of free space

The voltage is the product between the distance and the electric field, then

`V = dE = (d\sigma)/(\epsilon_0)`

`V = ((8*10^(-2)m)(2*10^(-9)C/m^2))/(8.85*10^(-12))`

`V = 18V`

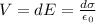
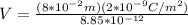
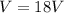
Therefore the magnitude of the electric potential is 18V