Answer:
The number of turns in the coil is 86.
Step-by-step explanation:
Given that,
The magnitude of maximum torque produced in the motor,
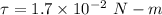
Area of the coil,

Current in the coil, I = 1.1 A
Magnetic field in the coil, B = 0.2 T
We need to find the value of N i.e. number of turns in the coil. The magnitude of torque attained in the coil is given by :

Here,
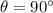 (maximum)
(maximum)
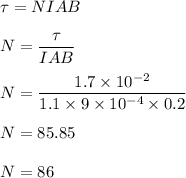
So, the number of turns in the coil is 86. Hence, this is the required solution.