Answer:
0.03605 V/m is the electric field in the gold wire.
Step-by-step explanation:
Resistivity of the gold =
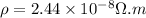
Length of the gold wire = L = 14 cm = 0.14 m ( 1 cm = 0.01 m)
Diameter of the wire = d = 0.9 mm
Radius of the wire = r = 0.5 d = 0.5 × 0.9 mm = 0.45 mm =
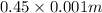
( 1mm = 0.001 m)
Area of the cross-section =
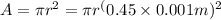
Resistance of the wire = R
Current in the gold wire = 940 mA = 0.940 A ( 1 mA = 0.001 A)
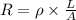
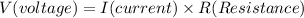 ( Ohm's law)
( Ohm's law)
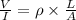
We know, Electric field is given by :
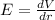
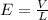
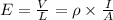
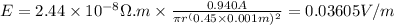
0.03605 V/m is the electric field in the gold wire.