Question

A space station shaped like a giant wheel has a radius of a radius of 153 m and a moment of inertia of 4.16 × 10⁸ kg·m² (when it is unmanned). A crew of 150 live on the rim, and the station is rotating so that the crew experience an apparent acceleration of 1g. When 100 people move to the center of the station, the angular speed changes. What apparent acceleration is experienced by the managers remaining at the rim? Assume that the average mass of each inhabitant is 65.0 kg. m/s².

Answer 1

a = 1.709g

Step-by-step explanation:

Given the absence of external forces being applied in the space station, it is possibly to use the Principle of Angular Momentum Conservation, which states that:

`I_(o) \cdot \omega_(o) = I_(f) \cdot \omega_(f)`

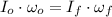
The required initial angular speed is obtained herein:

`g= \omega_(o)^(2)\cdot R_(ss)`

`\omega_(o)=\sqrt{(g)/(R_(ss)) }`

`\omega_(o)= \sqrt{(9.807\,(m)/(s^(2)) )/(153\,m) }`

`\omega_(o) \approx 0.253\,(rad)/(s)`

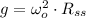
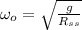
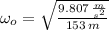
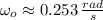
The initial moment of inertia is:

`I_(o) =I_(ss)+n\cdot m_(person)\cdot R_(ss)^(2)`

`I_(o) = 4.16* 10^(8)\,kg\cdot m^(2)+(150)\cdot (65\,kg)\cdot (153\,m)^(2)`

`I_(o) = 6.442* 10^(8)\,kg\cdot m^(2)`

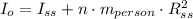
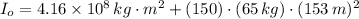
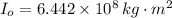
The final moment of inertia is:

`I_(f) =I_(ss)+n\cdot m_(person)\cdot R_(ss)^(2)`

`I_(f) = 4.16* 10^(8)\,kg\cdot m^(2)+(50)\cdot (65\,kg)\cdot (153\,m)^(2)`

`I_(f) = 4.921* 10^(8)\,kg\cdot m^(2)`

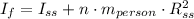
Now, the final angular speed is obtained:

`\omega_(f) = (I_(o))/(I_(f))\cdot \omega_(o)`

`\omega_(f) = \frac{6.442* 10^(8)\,{kg\cdot m^(2)}}{4.921* 10^(8)\,kg\cdot m^(2)} \cdot (0.253\,(rad)/(s) )`

`\omega_(f) = 0.331\,(rad)/(s^)`

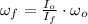
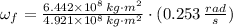
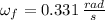
The apparent acceleration is:

`a_(f) = \omega_(f)^(2)\cdot R_(ss)`

`a_(f) = (0.331\,(rad)/(s) )^(2)\cdot (153\,m)`

`a_(f) = 16.763\,(m)/(s^(2))`

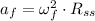
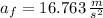
This is approximately 1.709g.