Answer:
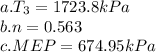
Step-by-step explanation:
a. Internal energy and the relative specific volume at
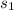 are determined from A-17:
are determined from A-17:
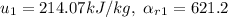 .
.
The relative specific volume at
 is calculated from the compression ratio:
is calculated from the compression ratio:
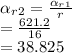
#from this, the temperature and enthalpy at state 2,
 can be determined using interpolations
can be determined using interpolations
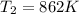 and
and
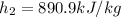 . The specific volume at
. The specific volume at
 can then be determined as:
can then be determined as:
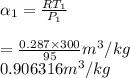
Specific volume,
 :
:
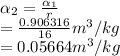
The pressures at
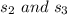 is:
is:
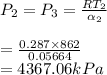
.The thermal efficiency=> maximum temperature at
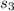 can be obtained from the expansion work at constant pressure during
can be obtained from the expansion work at constant pressure during

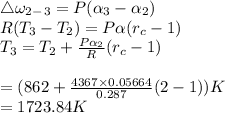
b.Relative SV and enthalpy at
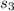 are obtained for the given temperature with interpolation with data from A-17 :
are obtained for the given temperature with interpolation with data from A-17 :

Relative SV at
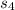 is
is
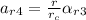
=
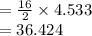
Thermal efficiency occurs when the heat loss is equal to the internal energy decrease and heat gain equal to enthalpy increase;
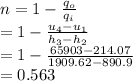
Hence, the thermal efficiency is 0.563
c. The mean relative pressure is calculated from its standard definition:
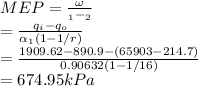
Hence, the mean effective relative pressure is 674.95kPa