Answer:
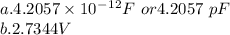
Step-by-step explanation:
a.
Given the permittivity constant to be
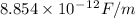 ,The capacitance of a
,The capacitance of a
 of length,
of length,
 is given by the equation:
is given by the equation:
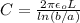 where
where
 is the radius of the outer cylinder and
is the radius of the outer cylinder and
 the radius of the inner cylinder.
the radius of the inner cylinder.
The values are given as:

Substitute in our capacitance equation:

Hence the capacitance is
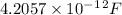
b. The charge on the capacitance is related to the potential difference across it. The potential difference is expressed using the equation:
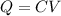 ,
,
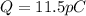
From a above, we already have our capacitance value,
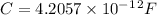
We substitute
 in the pd equation:
in the pd equation:
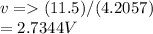
Hence, the applied potential difference is 2.7344V