Question

Mike buys a perpetuity-immediate with varying annual payments. During the first 5 years, the payment is constant and equal to 10. Beginning in year 6, the payments start to increase. For year 6 and all future years, the payment in that year is K% larger than the payment in the year immediately preceding that year, where K < 9.2. At an annual effective interest rate of 9.2%, the perpetuity has a present value of 167.50. Calculate K.

Answer 1

According to the given data we have:

i = 0.092

167.5 = 10a5] at .092 + v^5{10[(1+k)/1.092].....for infinity}

After the 10a5] at .092 component gone from the problem, we have:

128.804 = 10
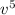`v^(5)`[(1+k) +
`(1+k)^(2)`v + (1+k)
`^(3)`
`v^(2)`.....for infinity}

You can turn this into a geometric progression by pulling out

10 * [(1+k)/1.092]...then your left with 1 + (1+k)/1.092 + (1+k)^2/1.092^2....for infinity.

Since the problem says k < .092.. you know that (1+k)/1.092 is eventually going to converge to 0.

Therefore, you'll have 1/(1-(1+k)/1.092) as your geometric sum.

That geometric sum * (10*v^6*(1+K)) then has to equal your constant, 128.804.

After dividing 128.804 by 10*v^6 you get 21.84.

21.84 = (1+k)*[1/(1-(1+k)/1.092)

Solving for (1+k), you get 1.04 so k = .04 or 4%