Question

A chemical reaction takes place inside a flask submerged in a water bath. The water bath contains 8.10kg of water at 33.9 degrees celsius . During the reaction 69.0kJ of heat flows out of the bath and into the flask.Calculate the new temperature of the water bath. You can assume the specific heat capacity of water under these conditions is 4.18J*g*K. Round your answer to 3 significant digits.

Answer 1

The new temperature of the water bath 32.0°C.

Step-by-step explanation:

Mass of water in water bath ,m= 8.10 kg = 8100 g ( 1kg = 1000g)

Initial temperature of the water =
`T_1=33.9^oC=33.9+273K=306.9 K`

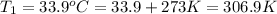
Final temperature of the water =
`T_2`

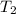
Specific heat capacity of water under these conditions = c = 4.18 J/gK

Amount of energy lost by water = -Q = -69.0 kJ = -69.0 × 1000 J

( 1kJ=1000 J)

`Q=m* c* \Delta T=m* c* (T_2-T_1)`

`-69.0* 1000 J=8100 g* 4.18 J/g K* (T_2-306.9 K)`

`-69,000.0 J=8100 g* 4.18 J/g K* (T_2-306.9 K)`

`T_2=304.86 K=304.86 -273^oC=31.86^oC\approx 32.0^oC`

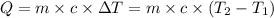
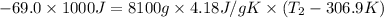
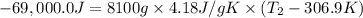
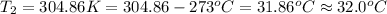
The new temperature of the water bath 32.0°C.