Question

Messages arrive to a computer server according to a Poisson distribution with a mean rate of 11 per hour. Determine the length of an interval of time (in seconds) such that the probability that no messages arrive during this interval is 0.76. Round your answers to one decimal place (e.g. 98.7).

Answer 1

The length of the interval during which no messages arrive is 90 seconds long.

Explanation:

Let X = number of messages arriving on a computer server in an hour.

The mean rate of the arrival of messages is, λ = 11/ hour.

The random variable X follows a Poisson distribution with parameter λ = 11.

The probability mass function of X is:

`P(X=x)=(e^(-11)11^(x))/(x!);\ x=0,1,2,3....`

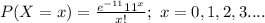
It is provided that in t hours the probability of receiving 0 messages is,

P (X = 0) = 0.76

Compute the value of t as follows:

`P(X=0)=(e^(-11* t)(11* t)^(0))/(0!)\\0.76=e^(-11* t)\\\ln(0.76)=-11* t\\t=-(\ln(0.76))/(11) \\=0.025\ hours\\\approx90\ seconds`

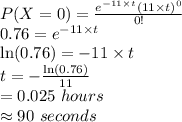
Thus, the length of the interval during which no messages arrive is 90 seconds long.