Question

A cracker manufacturer’s boxes have been found to have a standard deviation of 10 grams and a mean of 412 grams.

How many grams should be specified (printed on the box) to ensure that 95 percent of the boxes will contain more than this weight?

Answer 1

395.55 grams should be specified to ensure that 95 percent of the boxes will contain more than this weight.

Step-by-step explanation:

We are given the following information in the question:

Mean, μ = 412 grams

Standard Deviation, σ = 10 grams

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

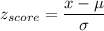
We have to find the value of x such that the probability is 0.95

P(X > x)

`P( X > x) = P( z > \displaystyle(x - 412)/(10))=0.95`

`= 1 -P( z \leq \displaystyle(x - 412)/(10))=0.95`

`=P( z \leq \displaystyle(x - 412)/(10))=0.05`

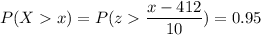
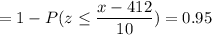
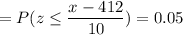
Calculation the value from standard normal z table, we have,

`\displaystyle(x - 412)/(10) = -1.645\\\\x = 395.55`

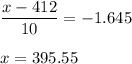
Hence, 395.55 grams should be specified to ensure that 95 percent of the boxes will contain more than this weight.