Question

A scene in a movie has a stuntman falling through a floor onto a bed in the room below. The plan is to have the actor fall on his back, but a researcher has been hired to investigate the safety of this stunt. When the researcher examines the mattress, she sees that it effectively has a spring constant of 77144 N/m for the area likely to be impacted by the stuntman, but it cannot depress more than 13.11 cm without injuring him. To approach this problem, consider a simplified version of the situation. A mass falls through a height of 4.12 m before landing on a spring of force constant 77144 N/m. Calculate the maximum mass that can fall on the mattress without exceeding the maximum compression distance.

Answer 1

131 kg

Step-by-step explanation:

Data:

Given,

spring constant, k = 65 144 N/m

Height of the fall = 3.32 m

Spring compression distance, x = 13. 55 × 10⁻²m

acceleration due to gravity, g = 9.81 ms⁻²

Now, during the fall, the gravitational potential energy is translated to the kinetic energy.

The kinetic energy is then later absorbed by the spring which absorbs it as the spring potential energy or simply (SPE).

Thus, the equation becomes:

Potential energy = Spring potential energy

`mh (h + x) = (1)/(2) kx^(2) \\m(9.81 * (3.32 + 0.1311) = (1)/(2)*65 144 * (0.1311)^(2) \\4.268 m = 559.82\\ m = 131 kg`

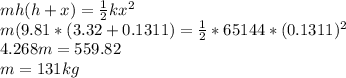
maximum mass = 131 kg