Question

Block B (mass 7.50 kg ) is at rest at the edge of a smooth platform, 2.60 m above the floor. Block A (mass 4.00 kg ) is sliding with a speed of 8.00 m/s along the platform toward block B. A strikes B and rebounds with a speed of 2.00 m/s. The collision projects B horizontally off the platform.

What is the speed of B just before it strikes the floor?

Answer 1

speed of block B after collision is 5.33 m/s

speed of block B before strike speed 8.9 m/s

Step-by-step explanation:

given data

mass = 7.50 kg

height = 2.60 m

speed =8.00 m/s

rebound speed = 2.00 m/s.

solution

we will apply here conservation of momentum that is

m1v1 + m2v2 = m1vr + m2v .................1

4 × 8 + 7.50 × 0 = 4 × (-2) + 7.50 × v

solve it we get

v = 5.33 m/s

so here speed of block B after collision is 5.33 m/s

and

and now by conservation of energy

we get here strike speed that is

PE(i) + KE(i) = PE(f) + KE(f) ..............2

m×g×h + 0.5 × m × (v(i))² = 0 + 0.5 ×m×(v(f))²

m ( g×h + 0.5×(v(i))²) = 0.5 ×m×(v(f))²

9.8 × 2.60 + 0.5 × 5.33² = 0.5 × (v(f))²

solve it we get

v(f)² =
`(39.7)/(0.5)`

v(f) =
`\sqrt{(39.7)/(0.5)}`

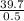
v(f) = 8.9 m/s

so speed of block B before strike speed 8.9 m/s