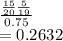Answer:
Explanation:
Given that a manufacturing firm just received a shipment of 20 assembly parts, of slightly varied sizes, from a vendor. The manager knows that there are only 15 parts in the shipment that would be suitable.
a) The probability that the first part is suitable.
= no of suitable/total =

b) the probability that the second part is also suitable/first part was suitable
= Prob that first two parts suitable/Prob first part suitable
=
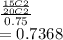
c) If the first part is suitable, find the probability that the second part is not suitable
= Prob I part suitable and second not suitable/Prob first part suitable
=