Question

Use the properties of limits to help decide whether each limit exists. If limit exits, find its value.

a. lim_x-->[infinity] x^4 - x^3 - 3x / 7x^2 + 9
b. lim_x-->25 √x - 5 / x - 25

Answer 1

a) The limit doesnt exist.

b) The limit exists and its value is 1/10

Explanation:

a) We take the highest power (x⁴) as common factor in both the numerator and the denominator.

`\lim_(x \to \infty) (x^4-x^3-3x)/(7x^2+9) = \lim_(x \to \infty) (x^4(1-1/x-3/x^3))/(x^4(7/x^2+9/x^4)) = \lim_(x \to \infty) (1-1/x-3/x^3)/(7/x^2+9/x^4)`

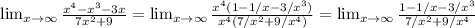
The limit of the numerator is 1 (when x goes to infinity) and the limit on the second part is 0. Hence the limit doesnt exist (it goes to infinity).

b) Note that if we multiply √x - 5 by its conjugate of , which is √x + 5, we obtain x - 25, thus

`\lim_(x \to 25) (\sqrt x - 5)/(x - 25) = \lim_(x \to 25) ((√(x) - 5))/((√(x) - 5) * (√(x)+5)) = \lim_(x \to 25) (1)/(\sqrt x + 5) = (1)/(5+5) = (1)/(10)`

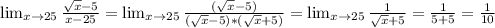
Hence, the limit exists and its value is 1/10.