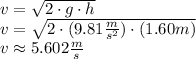Answer:
v ≈ 5.602 m/s
Step-by-step explanation:
By applying Work-Energy Theorem and Principle of Energy Conservation, the physical model of given system is described below. It is assumed that height at the bottom is zero:

Where
 and
and
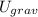 are the kinetic energy and gravitational potential energy, respectively.
are the kinetic energy and gravitational potential energy, respectively.
Initial velocity is found by isolating in that equation.