Question

A Finance professor created a multiple-choice examination with 100 questions for his students. Each question has five possible answers. Assume that a student who has done the homework and attended lectures has an 85% probability of answering any question correctly.

a. A student must answer 90 or more questions correctly to obtain a grade of A. What percentage of the students who have done their homework and attended lectures will obtain a grade of A on this multiple choice examination?
b. A student who answers 77 to 83 questions correctly will receive a grade of C. What percentage of students who have done their homework and attended lectures will obtain a grade of C on this multiple choice examination?
c. A student must answer 73 or more questions correctly to pass the examination. What percentage of the students who have done their homework and attended lectures will pass the examination?
d. If a student does not pass the examination but the student answers 28 or more questions correctly, the student can appeal to take another new examination. If pass, the highest grade can only be a passing grade, say D. Assume that a student has not attended class and has not done the homework for the course. Furthermore, assume that the student will simply guess at the answer to each question. What is the probability that this student will answer 28 or more questions correctly and have an opportunity to appeal to take another new examination?

Answer 1

a. 0.011 or 1.1%

b. 31.56% or 0.3156

c. 99.94% or 0.9994

d. 3.42% or 0.0342

Explanation:

Given

Number of multiple choice questions = 100

Probability of success for students who have attended lectures and done their homework = 0.85

a. Using binomial distribution

Probability of correctly answering 90 or more questions out of 100

`= \sum^(100)_(x=90)\left {100} \atop {x}} \right C (0.85)^x(0.15)^(100-x)\\=0.011`

Since,

In Binomial Distribution

`P(X=x) =\left {h} \atop {x}} \right.C P^x q^(n-x)`

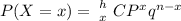
where
`x=0,1,...,n`

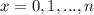
and
`q=1-P`

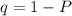
Probability is therefore 1.1% or 0.011

b. Probability of correctly answering 77 to 83 questions out of 100

`= \sum^(83)_(x=77)\left {100} \atop {x}} \right C (0.85)^x(0.15)^(100-x)\\=0.3156`

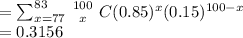
The probability is therefore 31.56% or 0.3156

c. Probability of correctly answering more than 73 questions out of 100

`= \sum^(100)_(x=73)\left {100} \atop {73}} \right C (0.85)^x(0.15)^(100-x)\\=0.9994`

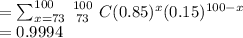
The probability is therefore 99.94% or 0.9994

d. Assuming that the student has answered randomly

Probability of success = 1/5 = 0.2

Probability of failure = 1 - 0.2 = 0.8

Probability of answering 28 or more questions correctly

`= \sum^(100)_(x=28)\left {100} \atop {x}} \right.c (0.2)^x(0.8)^(100-x)\\=0.0342`

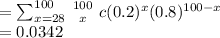
The probability is therefore 3.42%