Question

Assume that your parents wanted to have $150,000 saved for college by your 18th birthday and they started saving on your first birthday. They saved the same amount each year on your birthday and earned 12.0% per year on their investments.

a. How much would they have to save each year to reach their​ goal?

Answer 1

`\large\boxed{\large\boxed{\$2,690.60}}`

Step-by-step explanation:

The situation described corresponds to a constant annuity for a series of years. This is the value of a series of annual contant payments, at a constant rate.

The formula to calculate the future value of constant annuity, starting a year from today, is:

`FV_(annuity)=((1+r)^n-1)/(r)* annual\text{ }investment`

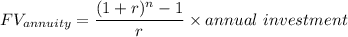
Where:

• r is the constant interest rate: 12.0% = 0.12

• n is the number of years: 18

• 
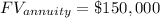  `FV_(annuity)=\$150,000` (the goal)

• Annual investment: is the amount they have to save each year to reach their goal.

Substitute and solve for tha annual investment:

`\$150,000=((1+0.12)^(18)-1)/(0.12)* annual\text{ }investment\\\\\\annual\text{ }investment=\$150,000/55.749715=\$2,690.60`