Question

Consider point C(−4, 2, 5) and the plane of equation 2x + 5y − 4z = 5. (a) Find the radius of the sphere with center C tangent to the given plane. (b) Find point P of tangency

Answer 1

Explanation:

C is a point (-4,2,5)

Plane is 2x+5y -4z =5 and the sphere with centre at C touches this plane.

Equation of C from this plane would be radius of the sphere.

Radius =

=
`|(2(-4)+5(2)-4(5)-5)/(√(2^2+5^2+4^2) ) |\\=(23)/(√(45) )`

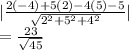
Centre is (-4,2,5)

If (x,y,z) is a general point in the sphere, distance between (x,y,z) and (-4,2,5) would equal radius.

i.e.

`(x+4)^2+(y-2)^2+(z-5)^2 = (529)/(45)`

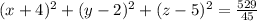
is the sphere equation.