Question

The percent of fat calories that a person consumes each day is normally distributed with a mean of 35 and a standard deviation of 10. Suppose that 16 individuals are randomly chosen. Let X = average percent of fat calories. (a) For the group of 16 individuals, find the probability that the average percent of fat calories consumed is more than thirty-seven. (Round your answer to four decimal places.) b) Find the first quartile for the average percent of fat calories. (Round your answer to two decimal places.) percent of fat calories

Answer 1

a) 0.2119 = 21.19% probability that the average percent of fat calories consumed is more than thirty-seven.

b) The first quartile for the average percent of fat calories is 33.31

Explanation:

To solve this question, we have to understand the normal probability distribution and the central limit theorem.

Normal probability distribution:

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

Central limit theorem:

The Central Limit Theorem estabilishes that, for a random variable X, with mean
`\mu` and standard deviation
`\sigma`, a large sample size can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`

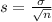
In this problem, we have that:

`\mu = 35, \sigma = 10, n = 16, s = (10)/(√(16)) = 2.5`

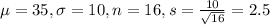
(a) For the group of 16 individuals, find the probability that the average percent of fat calories consumed is more than thirty-seven. (Round your answer to four decimal places.)

This is the 1 subtracted by the pvalue of Z when X = 37. So

`Z = (X - \mu)/(\sigma)`

By the Central Limit Theorem

`Z = (X - \mu)/(s)`

`Z = (37 - 35)/(2.5)`

`Z = 0.8`

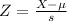
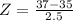
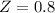
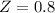`Z = 0.8` has a pvalue of 0.7881

1 - 0.7881 = 0.2119

0.2119 = 21.19% probability that the average percent of fat calories consumed is more than thirty-seven.

b) Find the first quartile for the average percent of fat calories. (Round your answer to two decimal places.) percent of fat calories

The 1st quartile is the 25th percentile. So this is the value of X when Z has a pvalue of 0.25. So it is X when Z = -0.675. So

`Z = (X - \mu)/(s)`

`-0.675 = (X - 35)/(2.5)`

`X - 35 = -0.675*2.5`

`X = 33.31`

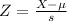
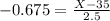
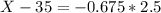
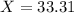
The first quartile for the average percent of fat calories is 33.31