Answer:
n = 1
Explanation:
We need to solve this equation for "n".
We first have to recognize the denominator and numerator as a "same" base number.
We know that 216 and 36 can be written as powers of 6. So, we write:
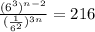
Now, we can write the denominator using the rule:
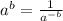
So, it becomes:
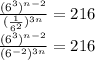
Now, we can use the rule:
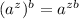
So, we have:

When we have same base, we can write it together using the identity:
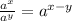
Thus,
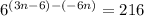
Writing RHS as 6^3 and solving, we have:
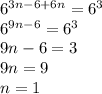
Thus,
n = 1