Answer:
Percentage of scores that fall between 70 and 80 = 24.34%
Explanation:
We are given a test with a population mean of 75 and standard deviation equal to 16.
Let X = Percentage of scores
Since, X ~ N(
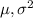 )
)
The z probability is given by;
Z =
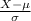 ~ N(0,1) where,
~ N(0,1) where,
 = 75 and
= 75 and
 = 16
= 16
So, P(70 < X < 80) = P(X < 80) - P(X <= 70)
P(X < 80) = P(
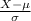 <
<
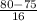 ) = P(Z < 0.31) = 0.62172
) = P(Z < 0.31) = 0.62172
P(X <= 70) = P(
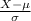 <
<
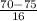 ) = P(Z < -0.31) = 1 - P(Z <= 0.31)
) = P(Z < -0.31) = 1 - P(Z <= 0.31)
= 1 - 0.62172 = 0.37828
Therefore, P(70 < X < 80) = 0.62172 - 0.37828 = 0.24344 or 24.34%