Question

Ammonia will decompose into nitrogen and hydrogen at high temperature. An industrial chemist studying this reaction fills a 7.50 l tank with 29.0 mol of ammonia gas at 35.0 °C. She then raises the temperature, and when the mixture has come to equilibrium measures the amount of nitrogen gas to be 13.0 mol.

Calculate the concentration equilibrium constant for the decomposition of ammonia at the final temperature of the mixture. Round your answer to significant digits.

Answer 1

Answer: The equilibrium constant for the reaction is 2.47

Step-by-step explanation:

We are given:

Initial moles of ammonia gas = 29.0 moles

Equilibrium moles of nitrogen gas = 13.0 moles

Volume of the tank = 7.50 L

Molarity is calculated by using the formula:

`\text{Molarity}=\frac{\text{Number of moles}}{\text{Volume of tank}}`

`\text{Initial molarity of ammonia}=(29.0)/(7.50)=3.87M`

`\text{Equilibrium molarity of nitrogen gas}=(13.0)/(7.50)=1.73M`

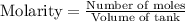
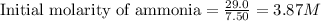
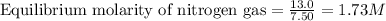
The chemical equation for the decomposition of ammonia follows:

`2NH_3\rightleftharpoons N_2+3H_2`

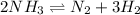
Initial: 3.87

At eqllm: 3.87-2x x 3x

Evaluating the value of 'x'

`\Rightarrow 3x=1.73\\\\x=(1.73)/(3)=0.577`

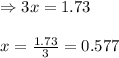
So, equilibrium concentration of ammonia = (3.87 - 2x) = [3.87 - 2(0.577)] = 2.716 M

Equilibrium concentration of nitrogen gas = x = 0.577 M

The expression of
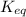`K_(eq)` for above equation follows:

`K_(eq)=([N_2][H_2]^3)/([NH_3]^2)`

Putting values in above equation, we get:

`K_(eq)=((2.716)^2)/(0.577* (1.73)^3)\\\\K_(eq)=2.47`

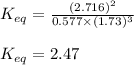
Hence, the equilibrium constant for the reaction is 2.47