Question

A catapult is designed to launch circus performers from a raised platform. After launch, the height of the performer in feet is given by h left parenthesis t right parenthesis equals minus 16 t squared plus 80 t plus 32 where t is seconds after launch. After how many seconds is the performer exactly 100 feet above the ground? Round to the nearest tenth of a second.

Answer 1

t = 1.1 sec for first time and then in

t = 3.9 sec

Explanation:

The function for the height of the circus performers is:

`h(t) = -16t^(2) +80t +32`

where t is seconds after launch

h is height in feet

For calculating after how many seconds is the performer at 100 feet above the ground, we must equal the equation to 100 and to find t:

Then,

`100 = -16t^(2) +80t+32`

`0 = -16t^(2)+80t -68`

`t = \frac{-80\ \pm \\\sqrt{80^(2)-4(-16)(-68) } }{2(-16)}`

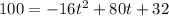
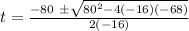
t = 3.9 sec

t = 1.1 sec