Question

The average (arithmetic mean) of three positive numbers is 10. One of the numbers is 12. The product of the other two numbers is 32. What is the greatest of the three numbers?

Answer 1

The greatest of the three number is 16.

Explanation:

We are given the following in the question:

Let x and y be the two numbers.

`\text{Mean} = (12+x+y)/(3) = 10\\\\12 + x + y = 30\\x + y = 18`

Also

`xy = 32`

Puting values, we get,

`x(18-x) = 32\\-x^2 + 18x - 32 = 0\\x^2 - 18x + 32 = 0\\(x-16)(x-2) = 0\\x = 16, x = 2`

When x = 16, y = 2

When x = 2, y = 16

Thus, the greatest of the three number is 16.

Answer 2

16

Explanation:

Let x and y be two numbers other than 12.

We have been given that the average (arithmetic mean) of three positive numbers is 10. We can represent this information in an equation as:

`(x+y+12)/(3)=10`

We are also told that the product of the other two numbers is 32. We can represent this information in an equation as:

`x\cdot y=32...(2)`

`x=(32)/(y)`

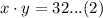
Upon substituting this value in above equation, we will get:

`((32)/(y)+y+12)/(3)=10`

`((32)/(y)\cdot y+y\cdot y+12\cdot y)/(3)=10\cdot y`

`(32+y^2+12y)/(3)=10y`

`(32+y^2+12y)/(3)\cdot 3=10y\cdot 3`

`32+y^2+12y=30y`

`y^2+12y-30y+32=30y-30y`

`y^2-18y+32=0`

`y^2-16y+2y+32=0`

`y(y-16)-2(y-16)=0`

`(y-16)(y-2)=0`

`y=2, 16`

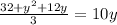
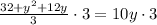
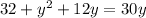
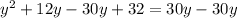
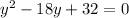
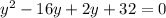
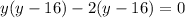
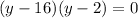
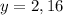
Since product of 2 and 16 is 32, therefore, the greatest of the three numbers would be 16.