Answer:
a) We have the following distribution
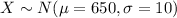
And we want to calculate:
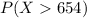
And in order to calclate this in the ti 84 we can use the following code
2nd> Vars>DISTR
And then we need to use the following code:
1-normalcdf(-1000,654,650,10)
And we got:
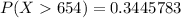
b) For this case we assume a normal standard distribution and we want to calculate:
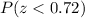
And using the following code in the Ti84 or using the normal standard table we got:
normalcdf(-1000,0.72,0,1)

So this part was the wrong solution from the solution posted,
Explanation:
Part a
We have the following distribution
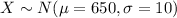
And we want to calculate:
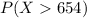
And in order to calclate this in the ti 84 we can use the following code
2nd> Vars>DISTR
And then we need to use the following code:
1-normalcdf(-1000,654,650,10)
And we got:
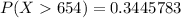
Part b
For this case we assume a normal standard distribution and we want to calculate:
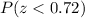
And using the following code in the Ti84 or using the normal standard table we got:
normalcdf(-1000,0.72,0,1)

So this part was the wrong solution from the solution posted,