Question

Darla and her friend penny left their office at the same time and began traveling down the same road in the same direction. Darla traveled at a speed of 65 mph while Penny drive at 70 mph. How many hours was it before Penny was 5 miles ahead of Darla?

Answer 1

The number of hours was it before Penny was 5 miles ahead of Darla is 1 hour.

Explanation:

Given : Darla and her friend penny left their office at the same time and began traveling down the same road in the same direction. Darla traveled at a speed of 65 mph while Penny drive at 70 mph.

To find : How many hours was it before Penny was 5 miles ahead of Darla?

Solution :

The formula used -
`\text{Distance}=\text{Speed}* \text{Time}`

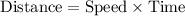
Darla traveled at a speed of 65 mph.

Penny drive at 70 mph.

Let x be the number of hours taken by both.

Distance covered by Darla is
`d_1= 65* x=65x`

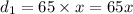
Distance covered by Penny is
`d_2= 70* x=70x`

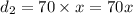
According to given statement; Penny was 5 miles ahead of Darla

i.e.
`d_2-d_1=5`

`70x-65x=5`

`5x=5`

`x=(5)/(5)`

`x=1`

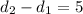
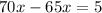
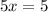
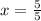
The number of hours was it before Penny was 5 miles ahead of Darla is 1 hour.