Question

In San Francisco, 30% of workers take public transportation daily. In a sample of 10 workers, what is the probability that exactly three workers take public transportation daily?

Answer 1

0.267

Explanation:

p = 0.3 q = 0.7

10C3 × p³ × q⁷

0.266827932

Answer 2

26.68% probability that exactly three workers take public transportation daily

Explanation:

For each worker, there are only two possible outcomes. Either they take public transportation daily, or they do not. The probability of a worker taking public transportation daily is independent from other workers. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

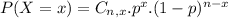
In which
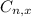`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

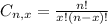
And p is the probability of X happening.

30% of workers take public transportation daily.

This means that
`p = 0.3`

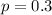
In a sample of 10 workers, what is the probability that exactly three workers take public transportation daily?

This is
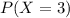`P(X = 3)` when
`n = 10`. So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 3) = C_(10,3).(0.3)^(3).(0.7)^(7) = 0.2668`

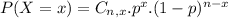
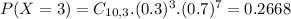
26.68% probability that exactly three workers take public transportation daily