Question

Events A1, A2 and A3 form a partiton of the sample space S with probabilities P(A1) = 0.3, P(A2) = 0.5, P(A3) = 0.2.

If E is an event in S with P(E|A1) = 0.1, P(E|A2) = 0.6, P(E|A3) = 0.8, compute

a. P(E) =
b. P(A1|E) =
c. P(A2|E) =
d. P(A3|E) =

Answer 1

a. By the law of total probability,

`P(E)=P(A_1\cap E)+P(A_2\cap E)+P(A_3\cap E)`

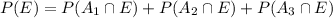
and using the definition of conditional probability we can expand the probabilities of intersection as

`P(E)=P(E\mid A_1)P(A_1)+P(E\mid A_2)P(A_2)+P(E\mid A_3)P(A_3)`

`P(E)=0.1\cdot0.3+0.6\cdot0.5+0.8\cdot0.2=0.49`

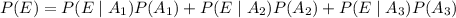
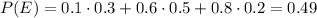
b. Using Bayes' theorem (or just the definition of conditional probability), we have

`P(A_1\mid E)=(P(A_1\cap E))/(P(E))=(P(E\mid A_1)P(A_1))/(P(E))`

`P(A_1\mid E)=(0.1\cdot0.3)/(0.49)\approx0.0612`

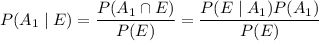
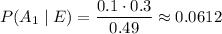
c. Same reasoning as in (b):

`P(A_2\mid E)=(P(E\mid A_2)P(A_2))/(P(E))\approx0.612`

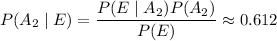
d. Same as before:

`P(A_3\mid E)=(P(E\mid A_3)P(A_3))/(P(E))\approx0.327`

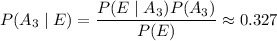
(Notice how the probabilities conditioned on
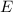`E` add up to 1)