Question

Which of the following are geometric sequences?
Check all that apply.​

Answer 1

The options A, B and C are geometric sequences whereas option D is not.

Explanation:

Step 1:

For a series to be a geometric sequence, the numbers in the series must be of a common multiplying ratio. So multiplying a constant value with any number will give the value of the next number.

The multiplying constant can be determined by;

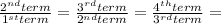`(2^(nd) term)/(1^(st) term) = (3^(rd) term)/(2^(nd) term) = (4^(th) term)/(3^(rd) term) =` The common multiplying ratio.

Step 2:

For option A, we determine the multiplying ratio,

`(2^(nd) term)/(1^(st) term) = (10)/(5) =2,`
`(3^(rd) term)/(2^(nd) term) = (20)/(10) =2, and`
`(4^(th) term)/(3^(rd) term) = (40)/(20) =2.`

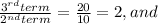
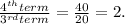
Since there is a common multiplying ratio of 2, option A is a geometric series.

Step 3:

For option B, we determine the multiplying ratio,

`(2^(nd) term)/(1^(st) term) = (5)/(10) =0.5,`
`(3^(rd) term)/(2^(nd) term) = (2.5)/(5) =0.5, and`
`(4^(th) term)/(3^(rd) term) = (2.5)/(1.25) =0.5.`

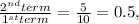
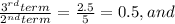
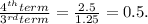
Since there is a common multiplying ratio of 0.5, option B is also a geometric series.

Step 4:

For option C, we determine the multiplying ratio,

`(2^(nd) term)/(1^(st) term) = (3)/(1) =3,`
`(3^(rd) term)/(2^(nd) term) = (9)/(3) =3, and`
`(4^(th) term)/(3^(rd) term) = (27)/(9) =3.`

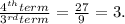
Since there is a common multiplying ratio of 3, option C is a geometric series.

Step 5:

For option D, we determine the multiplying ratio,

`(2^(nd) term)/(1^(st) term) = (6)/(3) =2,`
`(3^(rd) term)/(2^(nd) term) = (9)/(6) =1.5, and`
`(4^(th) term)/(3^(rd) term) = (12)/(9) =1.33.`

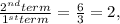
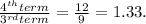
Since there is no common multiplying ratio, option D is not a geometric series.