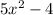The value of
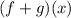 is
is
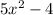
Step-by-step explanation:
Given that the functions
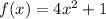 and
and
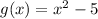
We need to determine the value of
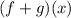
The value of
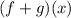 can be determined by substituting the value of
can be determined by substituting the value of
 and
and
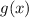 and simplifying the terms.
and simplifying the terms.
Thus, let us assign
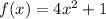 in the function
in the function
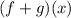 , we have,
, we have,
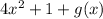
Now, let us assign
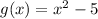 in the function
in the function
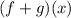 , we get,
, we get,
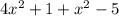
Grouping the like terms, we have,
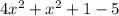
Adding the like terms, we get,
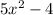
Hence, the value of
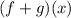 is
is