Question

If a farmer can trade four chickens for a pig, three pigs for two sheep, and five sheep for two cows, what is the minimum number of cows he needs to trade for $20$ chickens?

Answer 1

2

Explanation:

Answer 2

The minimum of cows he needs are: 2

Explanation:

There's a relation between each animal:

5 chickens equals 1 pig

3 pigs equals 2 sheep

5 sheep equals 2 cows

You can understand it as the following three abstractions:

5c = 1p (1)

3p = 2s (2)

5s = 2o (3)

Where:

c is for chickens

p is for pigs

s is for sheep

o is for cows

So now you have three equations with 4 variables. The next step is to obtain an equation that relates directly the variable c (chickens) with the variable o (cows). In order to do that from the equation 2 we obtain s in terms of p, as follow:

`3p =2s\\s=(3p)/(2) \\`

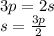
Then we replace s in the equation 3 and we obtain v in terms of p:

`5((3p)/(2) )=2v\\\\2v=(15)/(2) p\\\\`

`v=(15)/(2*2) p \\\\v=(15)/(4) p`

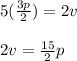
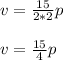
Now we replace v in the equation 1:

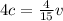
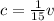`4c = (4)/(15) v`

`c=(1)/(15) v` (4)

The equation 4 means that 1 chicken equals the fifteenth part of a cow. For this case the farmer needs 20 chikens, so we multiply per 20 each part of the equation 4:

`20c = 20 * (1)/(15) v\\ \\\ 20c = (20)/(15)v = (4)/(3)v \\\\20c = 1.3333v`

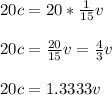
As it is impossible to have 1.3333 cows, the answer is 2 cows approximately.