Answer:

Step-by-step explanation:
The equation for the reaction is:
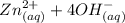 ⇄
⇄
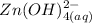
Oxidation can be defined as the addition of oxygen, removal of hydrogen and/or loss of electron during an electron transfer. Oxidation process occurs at the anode.
On the other hand; reduction is the removal of oxygen, addition of hydrogen and/ or the process of electron gain during an electron transfer. This process occurs at the cathode.
The oxidation-reduction process with its standard reduction potential is as follows:

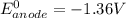
At the zinc electrode (cathode); the reduction process of the reaction with its standard reduction potential is :

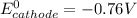
The standard cell potential
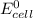 is given as:
is given as:
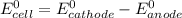
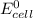 = -0.76 V - (- 1.36 V)
= -0.76 V - (- 1.36 V)
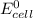 = -0.76 V + 1.36 V
= -0.76 V + 1.36 V
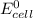 = +0.60 V
= +0.60 V
Now to determine the formation constant
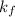 of the
of the
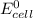 ; we use the expression:
; we use the expression:
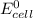 =
=
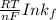
where;
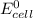 = +0.60 V
= +0.60 V
R = universal gas constant = 8.314 J/mol.K
T = Temperature @ 25° C = (25+273)K = 298 K
n = numbers of moles of electron transfer = 2
F = Faraday's constant = 96500 J/V.mol
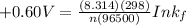
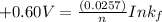
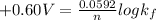
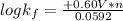
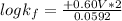
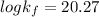
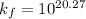
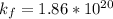
Therefore, the formation constant
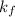 for the reaction is =
for the reaction is =
