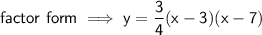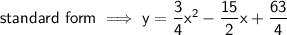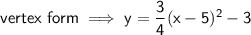Question

NEED AN ANSWER RIGHT NOW I HAVE ALMOST NO TIME PLEASE

The zeros of a quadratic relationship are 3 and 7. The optimal value is -3. Is the optimal value a maximum or minimum? Explain.
TYSM IF SOMEONE HELPS

Answer 1

Minimum

Explanation:

The zeros of a quadratic equation are the points at which the parabola intersects the x-axis.

`\sf x=3 \implies x-3=0`

`\sf x=7 \implies x-7=0`

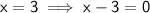
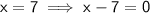
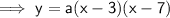`\sf \implies y=a(x-3)(x-7)` (for some constant a)

`\sf \implies y=ax^2-10ax+21a`

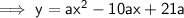
The optimal value is the y-coordinate of the vertex.

`\sf \implies vertex=(x,-3)`

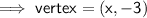
The x-coordinate of the vertex is the midpoint of the zeros:

`\sf x=(7-3)/(2)+3=5`

`\sf \implies vertex=(5,-3)`

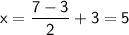
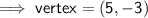
Therefore, the vertex will be in Quadrant IV and so the parabola opens upwards into Quadrant I.

So the optimal value is a MINIMUM since the vertex is the minimum point of the curve.

Additional Information to create the equation of the quadratic

Vertex form of quadratic equation:
`\sf y=a(x-h)^2+k`

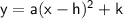
where (h, k) is the vertex

`\sf \implies y=a(x-5)^2-3`

`\sf \implies y=ax^2-10ax+25a-3`

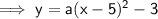
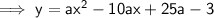
To find the value of a, compare the constants of both equations:

`\sf 21a=25a-3`

`\sf \implies -4a=-3`

`\sf \implies a=\frac34`

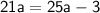
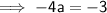
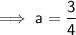
So the final equation is:

`\sf factor \ form \implies y=\frac34(x-3)(x-7)`

`\sf standard \ form\implies y=\frac34x^2-(15)/(2)x+(63)/(4)`

`\sf vertex \ form \implies y=\frac34(x-5)^2-3`