The radius R of the turn is 1.984 km.
Step-by-step explanation:
As the falcon is experiencing a centripetal motion, the acceleration exhibited by the falcon will be centripetal acceleration. The formula for centripetal acceleration is
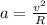
Here a is the acceleration for centripetal motion, v is the velocity and R is the radius of the circular path.
As the centripetal acceleration is given as 0.6 g, the velocity is given as 108 m/s, then the radius of the path can be determined as
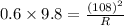
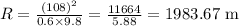
So, the radius of the turn is 1.984 km.