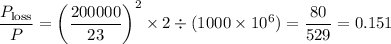Answer:
Current = 8696 A
Fraction of power lost =
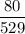 = 0.151
= 0.151
Step-by-step explanation:
Electric power is given by
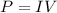
where I is the current and V is the voltage.

Using values from the question,

The power loss is given by

where R is the resistance of the wire. From the question, the wire has a resistance of
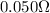 per km. Since resistance is proportional to length, the resistance of the wire is
per km. Since resistance is proportional to length, the resistance of the wire is

Hence,
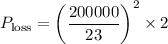
The fraction lost =