Answer:
D)191 feet
Explanation:
Let the height of the light house be |AB| and the Boat be at point C as shown in the diagram.
The angle of depression of the boat from the top A of the lighthouse is given as 25 degrees
Angle BCA = 25 degrees (Alternate Angles are Equal)
We want to determine the distance of the boat C from the base of the lighthouse B i.e. |BC|

Tan 25=
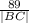
Cross multiply
|BC| X tan 25 =89
|BC| =
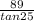 =190.86 feet
=190.86 feet
The distance of the boat C from the base of the lighthouse B is 191 feet (to the nearest feet).