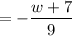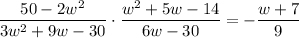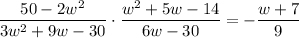
Solution:
Given expression:
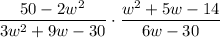
To solve the given expression:
First simplify:
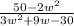
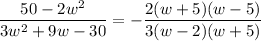
Cancel the common factor (w + 5).
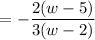
Now substitute this in the given expression.
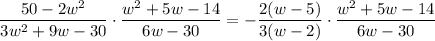
Multiply the fractions
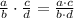
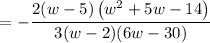
Factor the denominator
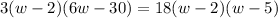
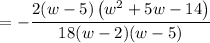
Cancel the common factor 2(w – 5).
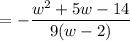
Factor the numerator
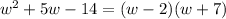
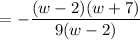
Cancel the common factor (w – 2).