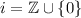Answer:
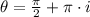 , for all
, for all
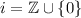
Explanation:
The velocity vector is found by deriving the position vector depending on the time:

In turn, acceleration vector is found by deriving the velocity vector depending on time:
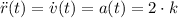
Velocity and acceleration vectors at
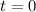 are:
are:
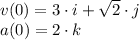
Norms of both vectors are, respectively:
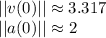
The angle between both vectors is determined by using the following characteristic of a Dot Product:
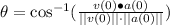
Given that cosine has a periodicity of
 . There is a family of solutions with the form:
. There is a family of solutions with the form:
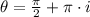 , for all
, for all