Question

A space station sounds an alert signal at time intervals of 1.00 h . Spaceships A and B pass the station, both moving at 0.400c0 relative to the station but in opposite directions.

Part A
How long is the time interval between signals according to an observer on A?
Part B
How long is the time interval between signals according to an observer on B?
Part C
At what speed must A move relative to the station in order to measure a time interval of 2.00 hbetween signals?

Answer 1

(A). The the time interval between signals according to an observer on A is 1.09 h.

(B). The time interval between signals according to an observer on B is 1.09 h.

(C). The speed is 0.866c.

Step-by-step explanation:

Given that,

Time interval = 1.00 h

Speed = 0.400 c

(A). We need to calculate the the time interval between signals according to an observer on A

Using formula of time

`\Delta t=\frac{\Delta t_(0)}{\sqrt{1-((v)/(c))^2}}`

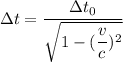
Put the value into the formula

`\Delta t=\frac{1.00}{\sqrt{1-((0.400c)/(c))^2}}`

`\Delta t=(1.00)/(√(1-(0.400)^2))`

`\Delta t=1.09\ h`

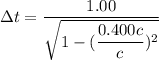
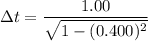
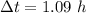
(B). We need to calculate the time interval between signals according to an observer on B

Using formula of time

`\Delta t=\frac{\Delta t_(0)}{\sqrt{1-((v)/(c))^2}}`

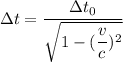
Put the value into the formula

`\Delta t=\frac{1.00}{\sqrt{1-((0.400c)/(c))^2}}`

`\Delta t=(1.00)/(√(1-(0.400)^2))`

`\Delta t=1.09\ h`

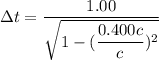
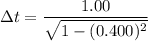
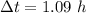
(C). Here, time interval of 2.00 h between signals.

We need to calculate the speed

Using formula of speed

`\Delta t=\frac{\Delta t_(0)}{\sqrt{1-((v)/(c))^2}}`

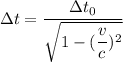
Put the value into the formula

`2.00=\frac{1.00}{\sqrt{1-((v)/(c))^2}}`

`\sqrt{1-((v)/(c))^2}=(1.00)/(2.00)`

`1-((v)/(c))^2=((1.00)/(2.00))^2`

`((v)/(c))^2=(3)/(4)`

`v=(√(3))/(2)c`

`v=0.866c`

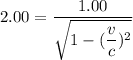
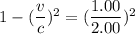
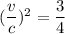
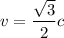
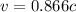
Hence, (A). The the time interval between signals according to an observer on A is 1.09 h.

(B). The time interval between signals according to an observer on B is 1.09 h.

(C). The speed is 0.866c.