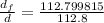Question

A circular copper wire is put in tension under a weight of 7000N. What is the ratio of its diameter after and before the load is applied, if the initial cross section of the wire is 0.01m2 and its Poisson ratio is 0.3

Answer 1

`(d_f)/(d) =0.9999983`

Step-by-step explanation:

Given:

• force applied on the copper wire,
  `F=7000\ N`

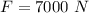
• cross sectional area of the wire,
  `a=0.01\ m^2`

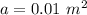
• Poisson's ratio,
  `\mu=0.3`

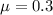
• we have, Young's modulus,
  `E=128* 10^3\ MPa`

Stress induced due to the applied force:

`\sigma=(F)/(a)`

`\sigma=(7000)/(0.01)`

`\sigma=700000\ Pa=0.7\ MPa`

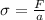
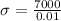
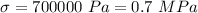
Now the longitudinal strain:

`\epsilon=(\sigma)/(E)`

`\epsilon=(0.7)/(128* 10^3)`

`\epsilon=5.468* 10^(-6)`

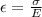
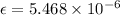
Now from the relation of Poisson's ratio:

`\mu=(\\u)/(\epsilon)`

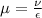
where:

`\\u=` lateral strain

`0.3=(\\u)/(5.468* 10^(-6))`

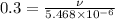
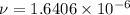`\\u=1.6406* 10^(-6)` ..................(1)

Now we find the diameter of the wire:

`a=\pi.(d^2)/(4)`

`0.01=\pi* (d^2)/(4)`

`(0.04)/(\pi) =d^2`

`d=0.1128\ m=112.8\ mm`

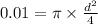
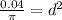
When the tensile load is applied its diameter decreases:

The lateral strain is also given as,

`\\u=(\Delta d)/(d)`

`1.6406* 10^(-6)=(\Delta d)/(112.8)`

`\Delta d=0.000185\ mm`

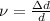
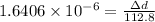
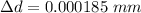
Now the final diameter will be:

`d_f=d-\Delta d`

`d_f=112.8-0.000185`

`d_f=112.799815\ mm`

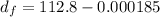
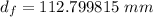
Now the ratio:

`(d_f)/(d) =(112.799815)/(112.8)`

`(d_f)/(d) =0.9999983`