Question

How long is the minor axis for the ellipse shown below?

(x+3)^2/64 + (y-7)^2/4=1

A. 16
B. 4
C. 8
D. 64

Imagine is shown above.

Answer 1

The length of the minor axis is 4

Explanation:

Step 1 :

The given equation is
`((x-3)^(2))/(64) + ((y-7)^(2))/(4) = 1`

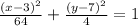
Here we see the denominator below the variable x is greater than below y. Hence the ellipse's major axis and the minor axis are parallel to x-axis and y-axis respectively

Step 2 :

The square of the semi minor axis will be the denominator of the y variable. So in the given ellipse ,

the square of the semi minor axis = 4

Hence the length of the semi minor axis =
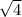`√(4)` = 2

Step 3 :

The length of the minor axis = 2 times the length of the semi minor axis

= 2 × 2 = 4

Answer :

The length of the minor axis is 4